負の周波数
「JOAKが300KWで送信しているとき、負の周波数でも300KWが放出されているのか」。大学時代に漠然と感じた疑問はこういったものでした。
正弦波の周波数と複素信号の周波数
われわれがオシロスコープを使って観測している電気信号は、すべて実信号です。つまり実数振幅をもつ電圧あるいは電流の振動です。正弦波の場合、位相を持ち込んで電圧を複素数表現することもありますが、実際にはそれは長い時間を考えたときのことであって、瞬時の信号値として位相情報を考えることには意味がありません。値はあくまで値であって、それ以上の情報を含んでいないのです。
実世界の信号値は実数です。したがって、図1(a)のような正弦波は、(b)のような1次元での電圧あるいは電流の振動ということになります(以下面倒なので信号電圧といった場合には電流でも同じです)。
図1 正弦波と単振動
このような信号を考えるとき、負の周波数とはどういうことか考えることができるでしょうか。位相がπ/2だけずれているのでしょうか。結論から言えばそうではありません。
実信号の周波数がたとえば594KHzだとしましょう。これはNHKラジオ第一放送東京放送局の周波数です。NHKラジオを聴いているとき、(この594KHzの反対の周波数ってどうなっているのだろう)と考えるのは実は無意味です。なぜならば、594KHzは正の周波数ではないからです。
なぜ、NHKラジオ第一の594KHzが正の周波数ではないか、図を見ながら説明しましょう。図1(b)のように一般の電気信号や電波は電圧や電界の単振動で考えることが出来ます。しかし、これらが正弦波であることから、さらに図2のように複素平面での二つの回転運動の合成と考えることが出来ます。これは条件付の合成ではないことに気をつけてください。正弦波はすべて二つの複素回転運動に分解でき、分解の前と後はまったく等価です。
二つの複素回転運動は時間とともに回転するため、時間軸を複素平面に垂直にとると、二つの螺旋としてあらわされます。螺旋を描く力がないため、図2には時間を省いた絵を使っています。
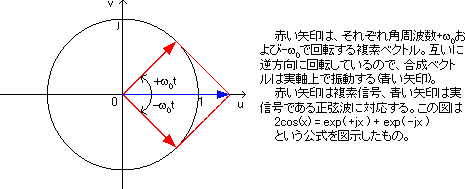
図2 正弦波の複素信号への分解
このとき二つの螺旋運動は回転速度が同じ(ω0)で、回転方向が異なります(+ω0と-ω0)。つまり回転方向に正負があります。もうお分かりだと思いますが、正の周波数、負の周波数とは角周波数+ω0と-ω0をそれぞれ2πで割ったもので、絶対値は回転速度を表します。そして正の周波数、負の周波数の正負とは複素平面上での回転方向を決める符号です。ですから、符号は実信号の性質とはなんら関係がありません。最初にあげた問いに対する答えを書くならばこんな感じになります。
JOAKは回転方向が異なる二つの複素信号波を放送しているとみなす事もできる。片方は+594KHz 150KWで、他方が-594KHz 150KWである。両者の合成は594KHz 300Wの実信号波となり、合成波の周波数に正負はない。
負の周波数とは、実世界の信号を複素信号の合成として捉えるときにだけ現れる概念なのです。ですから実信号の周波数に対して、符号が逆の周波数を考えることはできません。
なぜ複素信号が必要になるのか
複素信号を使う理由は何でしょうか。
- 瞬時の位相がわかるなどの解析信号としてのメリット。
- Weaver受信機のような回路を作り上げることが出来る。。
- フーリエ変換が複素信号に基づいている
最初の二つは使わなければ使わないでやっていけそうですが、最後のフーリエ変換だけは避けて通れません。そして良くご存知のように、フーリエ変換こそが、負の周波数などというものを生み出す元凶なのでした。
スペクトル解析に用いられるフーリエ変換は、もともとはラプラス変換同様に関数変換のひとつです。しかしながら元の関数を時間につれて変動する信号と見ると、フーリエ変換の結果を周波数スペクトルとしてみなすことが出来ます。そこで工学分野に広く使われているわけです。
フーリエ変換の式は以下のとおりです。
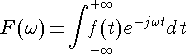
ここでe-jwtは、フーリエ変換の核で、ありていに言えば核がこの形をしているためにフーリエ変換から負の周波数が現れるといってかまいません。では、コサイン変換ではだめなのでしょうか。コサイン変換なら核は余弦関数であり、複素回転関数ではありませんから、回転方向を持ちません。負の周波数もいらないように思えます。しかしこれはうまくいきません。コサイン変換は解析したい関数が正弦波の場合、スペクトルが0になってしまいます。
フーリエ変換の核となっている指数関数は、変数が虚数のときに正規直交関数であり、かつ完全性を備えます。言い換えると、どんな関数も虚数を引数とする指数関数の組み合わせで表すことが出来ます。余弦関数にそのような性質はありません。
負の周波数は無視できるか
フーリエ変換に負の周波数がつき物だとしても、それを無視すればいいように思えます。しかしそうは問屋がおろしません。
たとえば正弦波と正弦波の積を考えます。このような場合、我々は結果の周波数が二つの正弦波の周波数の和と差であることを知っています。つまりf1, f2という周波数の正弦波の積は、f1 + f2, f1 - f2 になります。一方フーリエ変換の性質には次のようなものがあります。
- 正弦波のスペクトルはインパルス関数になる。
- 関数の積のフーリエ変換は、関数のフーリエ変換の畳み込み
このふたつから、正弦波の積のフーリエ変換は、正弦波のフーリエ変換の畳み込みになります。これはインパルス関数同士の畳み込みとなり、結果的にインパルス関数のずらし操作となります。位置がf1のインパルス関数は、位置がf2のインパルス関数と畳み込むことで位置がf1 + f2にずれます。
はて、f1 - f2のスペクトルはどこに行ったのでしょうか?f1とf2の畳み込みでは、f1 - f2 は出てきません。このスペクトルが現れるには - f2のスペクトルが元の信号に含まれていなければならないのです!
結局、あがいたところで負の周波数から逃げるわけには行きません。フーリエ変換が提示するスペクトルはきちんと自然の信号の振る舞いを反映しており、その中には負の周波数が織り込まれているのです。
負の周波数があることを認めましょう。ただしそれは実軸上の単振動の周波数ではなく、複素平面上の回転周波数なのです。
きちんと理解すれば使いでがある
負の周波数や複素信号処理の概念が異様だからといって、無理に逃げる必要はありません。むしろきちんと向き合うことで利点も生まれます。たとえば複素プロダクト検波で説明している複素フィルタなどそのひとつでしょう。むやみに恐れずに使うほうが賢いといえます。