ウェーバー式SSB変調は動作が難解だといわれます。ところが、信号を複素数として捕らえるとウェーバー方式はきわめて簡単に理解することができます。複素数であらわされる信号は解析信号と呼ばれ、瞬時の位相、振幅を求めることができるなどいろいろなメリットがあります。以下では解析信号によるウェーバー方式の検討を行います。
ウェーバー方式によるSSB変調回路のブロック図を図1に示します。
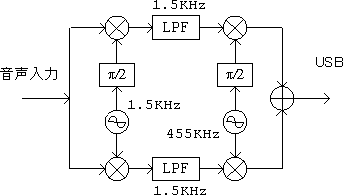
図1 ウェーバー方式SSB変調器
まずは入力部からはじめましょう。手始めに図1の第一乗算器までを取り扱います。ウェーバー方式の入力部を図2のように変形します。
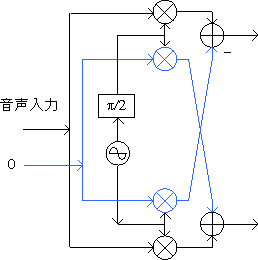
図2 変形した入力部
青い線が追加した部分です。黒い部分には加算器以外の追加や変更はありません。青い部分は入力が0であることから乗算器の出力は0となり、結局加算器の入力も0となります。そのため、青い部分の追加による処理の実質的な変更はありません。
さて、このような変更を施した結果、上の回路はどうなっったでしょうか。答えを先に言えば、元の回路では二つの実数乗算器だったものが、全体で一つの複素乗算器を持つ回路に変わっています。入力は(音声信号+j0)であり、第一局発(副搬送波)も複素数として扱うことができます。
第一局発をすこし詳しく見てみましょう。発振器が正弦波を生成すると、上に伸びるパス(実部)は+π/2だけ進むため、余弦となります。この結果、複素乗算器への副搬送波入力も複素数であらわすことができ、cos(2πf1t)+jsin(2πf1t)となります。これを変形すると最終的にej2πf1tとなります。
これらをまとめると、図2は図3のように複素乗算器と複素発振器に変形できます。
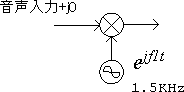
図3 入力部の複素表現
さて、こうして入力部は複素回路に変形できましたので、信号も複素信号としてみて見ましょう。入力信号から乗算器出力までを示したのが図4です。
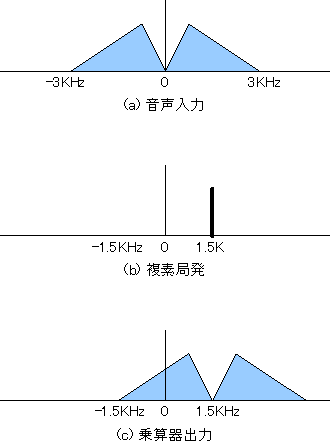
図4 信号の複素表現
図4を見ると、まず(a)の音声入力は通常どおり原点の両側に正のスペクトルと負のスペクトルが広がっています。しかし(b)の局発は様相が変わっています。通常ならば原点の両側にあるはずのスペクトルが正の側にしかありません。実はつきつめるとこちらのほうが基本的なスペクトルなのです。cos(x)=(exp(jx)+exp(-jx))/2 の関係からわかるように、一般に我々が基本的だと信じている正弦波(や、余弦波)は指数関数から合成できます。正弦波が正負にスペクトルを持つのは、じつはそれが合成波だからです。
負の周波数については別項「負の周波数」をご覧ください。
さて、このように局発の信号は正の側にだけスペクトルを持ちます。このような信号と音声入力を掛け合わせるとどうなるのでしょう。実空間での積はスペクトル空間では畳み込みになります。図4(b)のようなインパルス関数はずらし演算子として機能するため、結局音声スペクトルはずらされて図4(c)のようになります。
ここまでの結果をウェーバー式SSB変調と比べてわかるように、複素信号(解析信号)を使うとウェーバー方式から位相の考え方を追い出すことができます。そして、原点に対して非対称な信号処理を行っていることもわかります。
図1のフィルター部分は上のパス(今は実部であるとわかっています)と下のパス(虚部)でまったく同じです。これは複素信号に対して実数フィルターを施していることになります。このフィルターの周波数特性と、通過した信号を図5に示します。
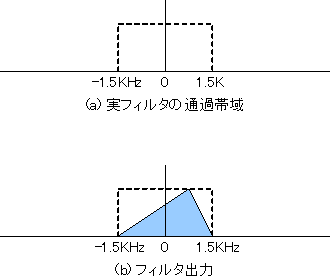
図5 フィルター部の信号
フィルターは実フィルターであるため、通過帯域は原点の左右に対称に広がります(a)。そのため遮断周波数1.5KHzのLPFは、複素信号としてみると通過帯域が-1.5KHzから1.5KHzになっています。一方、フィルターの入力部分では複素信号は正に1.5KHzシフトされています。したがって、フィルター出力は図5(b)のようになります。これは音声のスペクトルの正の部分を取り出し、周波数軸に沿って反転したものです。
最後に出力部を入力部同様複素数の視点で解釈します。まず、図6のように変形します。
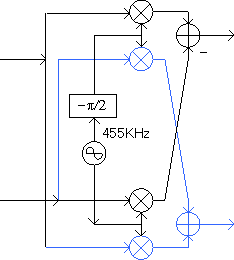
図6 変形した出力部
もうすでにご理解いただいていると思いますが、図6の乗算器は複素乗算器であり、第二局発も複素発振器です。ただし、複素乗算器に組み直すために図1の出力の加算器(図6の上側)が減算器に変更されています。この変更を行いつつ全体を等価に保つため、図6では位相シフトが正ではなく負になっています。このことから、発振器が生成する信号はe-j2πf2tになります。
図6の青い線が追加部分ですが、この回路の出力は単に捨てられます。青い線の回路は虚部の信号を処理しますので、結局実部だけを出力することになります。
信号のスペクトルを見てみましょう。
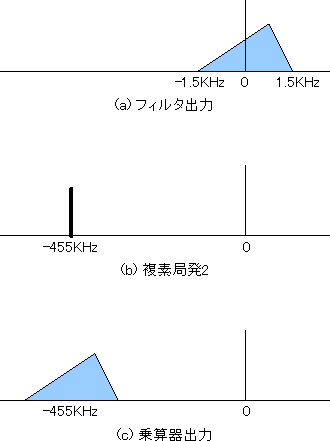
図7 出力部の信号スペクトル
出力部のスペクトルの処理は入力とよく似ています。図7(a)は前段の出力で、すでに説明したように音声スペクトルの片側だけが原点の両側に広がっています。図7(b)は第二局発のスペクトルです。この局発も複素信号を生成しますが、第一局発とちがって周波数は負です(指数関数の引数に負号がついている)。したがって、スペクトルも負側に一本立つだけです。乗算器はこれをシフト演算子として扱いますから、結局乗算器出力のスペクトルは図7(c)のように-455KHzのUSBとなります。周波数軸の正の半分にはなにもありません。
-455KHzの複素USBは、その虚部を取り去ると455KHzのUSBとなります。こうしてめでたくSSBを取り出すことができました。
複素信号(解析信号)の観点からウェーバー式SSB変調器を書き直すと図8のようになります。
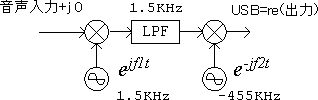
図8 ウェーバー式SSB変調器の複素表現
この非常に単純なブロックダイアグラムは、上に説明したように単純なスペクトル処理で説明可能です。その観点から考えると、ウェーバー方式とは図8の複素変調器のうち使わないパスを巧妙に省略して回路を簡略化した方式だとも言えます。
ウェーバー方式の複素表現に関しては、掲示板でハイフェッツさんに教えていただいた方式が大きなヒントになりました。この場を借りてお礼申し上げます。また、掲示板を読み直してみると昨年末にKESHさん、SiGeさんの御両方に複素信号や負の周波数に関する明快な説明をしていただいているにもかかわらず、まったく理解できていなかったのがわかります。さらにKV3NWVのサイトにもはっきりと同じ方法による説明がありながら、理解できずにいました。だめな学生は卒業してもだめだという見本かもしれません。
前回のウェーバー方式の実装の際には偶然にもJA1VCWが同時期にTIのDSPに実装していたという偶然がありましたが今回も奇妙な偶然がありました。
Ham Journal誌No.107は書店で表紙の「特集 メーカーが語る国産1KWリニアアンプの性能と実力」を一瞥して(俺には関係ないや)と購入を見送っていました。ところが、昨晩この稿の準備中にCQ出版社のサイトを見て同号にウェーバー方式の記事があることを発見。あわてて今日購入して読んで見ると、なんと記事はIV3NWVが開発したディジタル送信機の紹介です。私がウェーバー方式を実装するきっかけになったA 9MHz Digital SSB Modulatorの発展形です。しかも、記事の末尾には当サイトが参考文献として挙げられているという嬉しい事件もありました。編集さん、次回はURL掲載よろしく(^^)/
⇒次は複素周波数変換