包絡線を忘れよう
包絡線は、サンプル後のディジタル信号が実際のアナログ信号でどのようなものに再現されるかを連想させてくれる便利な補助線です。しかしこの包絡線を使うばっかりに、本当におきることを忘れてしまいがちです。
元信号とサンプリング
サンプリングとはどのようなものだったでしょうか。一言で言うと、「連続信号を離散時間信号に変換する操作」になります。ポイントは離散時間であって、デジタル化ではありません。よく誤解している方がいらっしゃいますが、デジタル化とは「離散時間・離散値」に変換することです。このうち離散時間への変換がサンプリングで、離散値への変換は量子化と呼ばれます。
サンプリングがどのように行われるか見てみましょう。図1に元信号を示します。
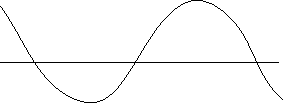
図1 元信号
この信号をサンプリングにかけると以下のような信号になります。
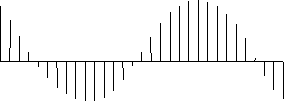
図2 サンプリング後
ここまではOKです。問題は、このサンプリング後の波形に包絡線を書き込む例が多いことです。
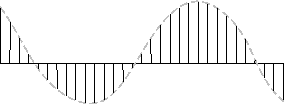
図3 包絡線を書き込んだ波形
包絡線は、サンプリング前の信号を明らかにするという意味でとても便利です。しかし、包絡線には大きな弊害があります。包絡線を描く事によって、読者は図2のサンプリング後の波形が図1の波形と等価であるという幻想を抱いてしまいかねません。図2のような刻まれた状態は仮の姿ではなく、図1の信号の別表現であるという錯覚です。
実際には、図2と図1の間の隔たりは極めて大きなものです。直感的に図2は図1の信号の瞬時の値を採取したものだと思いがちです。実際、「サンプリング」とはそのような言葉です。しかし、図2は表に書かれた数字の列ではなく、生きた信号なのです。
図2の正体は、図1の信号に図4のようなインパルス列を掛けたものです。
図4 インパルス列
インパレス列を掛けたということは、図2は図4を図1で変調した結果ということに他なりません。しつこく繰り返しますが、図2は採取されたデータを図示したものではなく、生きた波形そのものなのです。
したがって、当然のように図2の信号スペクトルは図1のそれとは異なります。
サンプルされた信号のスペクトル
包絡線を使うことによる弊害として最初に挙げるのは、サンプルした信号のスペクトルを想像しにくくなる点です。以下にサンプルされた信号のスペクトルを導き出しながら、包絡線の弊害がどの様なものか説明します。
図1の元信号のスペクトルを図5に、図4のインパルス列のスペクトルを図6に示します。Tsはインパルス列の周期で、これがサンプル周期となります。
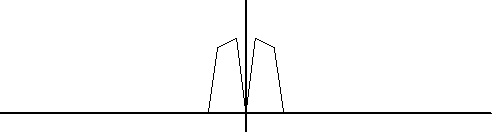
図5 元信号のスペクトル

図6 インパルス列のスペクトル
元信号とインパルス列の積のスペクトルは「時間軸での積は周波数軸での畳み込みになる」というフーリエ変換の性質を知っていれば簡単です。もちろん、スペクトルをもとに正弦波(余弦波)を取り出しておのおのの正弦波ごとに積を計算しても同じ結果になります。
得られる信号は以下のようになります。
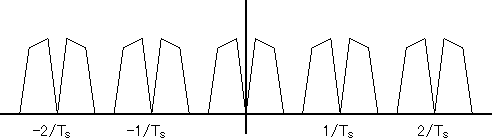
図7 サンプリング後のスペクトル
このように、サンプリング後のスペクトルは、元信号のスペクトルとは異なります。元信号が含まれているのは事実ですが、もはや単純に取り出せるわけではなく、何らかの操作が必要になるのは自明です。
上のスペクトルは信号処理の教科書では良くお目にかかります。しかし、このスペクトルは「サンプル波形のスペクトル」として提示されると大変理解しにくいものになります。サンプルという作業がスペクトルを変える理由がわからないためです。サンプルされれたデータを包絡線を通してみる限り、この部分を理解することは出来ません。しかし上で説明したようにサンプリングを離散時間化の手続きではなくアナログ信号操作として捉えれば、すぐに理解できます。
スペアナを持っているなら細いパルスの列を作ってアナログ乗算器に元信号と共に入力するといいでしょう。上のようなスペクトルの操作を眼で見ることが出来るはずです。そうすれば、サンプル後の信号が本質的に元信号と等価であるという幻想と決別しやすくなるでしょう。学生のうちに見ておけば余計な誤解をせずに済むと思うのですが、いかがでしょうか。
また、図7を見ると、「元信号のスペクトルは1/2Tsを超えて広がってはいけない」というナイキストの定理を直感的に理解できます。超えてしまうと、それぞれのスペクトルが重なりを持ってしまうため、元に戻せないのです。
アパーチャ効果
もうひとつ、包絡線の幻想を抱いていると理解しにくいものの例としてアパーチャ効果を挙げておきます。アパーチャ効果はDACの出力特性を悪化させる要素のひとつです。
図2の波形をDACで出力する場合を考えましょう。このとき、波形そのままにアナログインパルス出力を出すことが出来れば、その出力スペクトルは図7と同じものになります。あとは、ナイキスト周波数より高い成分を切り落とすローパスフィルタがあればよいことは自明です。しかし、DACの出力はインパルス列ではありません。
一般的なDACは出力にホールド回路を持っており、実際の出力波形は以下のようなステップ関数を連ねたものになります。
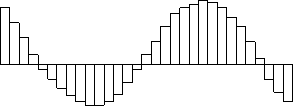
図8 現実のDACの出力波形
包絡線の幻想にとらわれていると、この波形に問題があることなど考えも付かないでしょう。何しろ包絡線の幻想に基づく限り、「サンプルされたデータは本質的に元データと等価」なのですから。しかし、実際にはこの幻想は儚くも消え去ります。信号処理の基礎が出来ていれば、図8の出力は、図2の波形を「矩形インパルス特性のフィルタ」にかけたものだと直ちに理解することが出来ます。そしてそのようなインパルス特性のフィルタは理想特性ではないのです。
その結果起きることを図9を見ながら説明します。
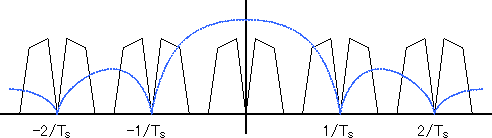
図9 アパーチャ効果による周波数特性の悪化
図9は、図2の波形のスペクトルに、矩形インパルス特性のフィルタの周波数特性を重ねたものです。青い点線が周波数特性です。このように矩形インパルス特性のフィルタは、ナイキスト周波数より下の領域でも平坦とは言いがたく、なだらかとはいえ周波数特性を悪化させることがわかります。
以上のようなDACの出力ホールド回路が起こす出力周波数特性の悪化をアパーチャ効果と呼びます。
包絡線の幻想にとらわれずに、図2を見ることが出来れば、図8が何かしらの変化を伴うだろう事は容易に理解できます。しかし、実際にこの理解が出来ていない人は多いようです。
包絡線を忘れよう
包絡線はAM変調の説明などで古くから使用されている補助線です。しかし、デジタル信号処理を学ぶ上で、包絡線にはいろいろな弊害があります。教科書に現れても早いうちに忘れて、信号をそのままの信号として捕らえることが出来るよう努力することをお奨めします。