複素周波数変換

ウェーバー方式の複素解釈で使用した複素乗算器と複素発振器について少し深く考察してみます。この二つを使った複素周波数変換器は、実数領域の周波数変換器に比べて面白い性質を持っています。

実数による周波数変換

はじめに実数による周波数変換について考えています。これは二つの実数信号を乗算器に掛けるもので、普通に通信機で使われるミキサーです。入力信号の周波数をf_S、局部発振器の周波数ををf_Lとすると、入力と局発のスペクトルはそれぞれ図1、2のようになります。

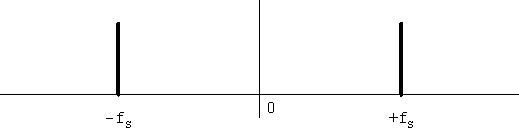
図1 入力信号のスペクトル

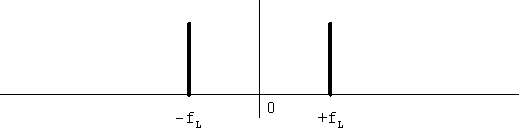
図2 局発のスペクトル

いずれの信号も実信号なので、スペクトルは正負に分裂します。入力信号は+f_Sと-f_Sに分裂し、局発信号は+f_Lと-f_Lに分裂します。

この二つの信号を実空間（時間領域）で掛け合わせるわけですが、これはスペクトル空間での畳み込みに相当します。畳み込みと考えると、図2は正負両方向へのずらし演算子と考えることができ、結局図1の信号は図3のように変換されます（図2の信号に図1のずらし演算子を適用すると考えても同じ）。

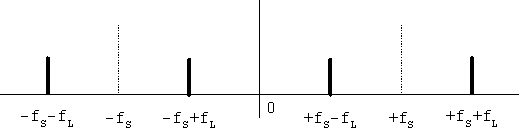
図3 周波数変換後のスペクトル

このように、周波数変換後のスペクトルは振幅変調波のスペクトルで行った三角関数の計算を行わなくとも求めることができます。

複素数による周波数変換

次に複素乗算器を使い、入力信号も局発も解析信号である場合を考えます。周波数はそれぞれ+f_Sと-f_Lであるとします（図4、図5）。

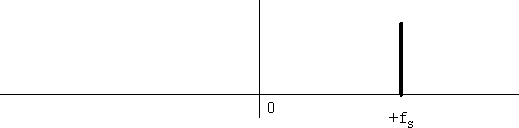
図4 入力信号のスペクトル

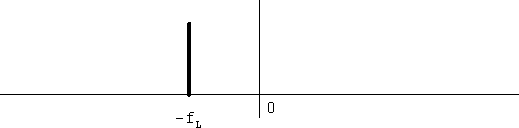
図5 局発信号のスペクトル

この場合、もともと入力信号も局発信号もスペクトルが一本であることから、出力の信号も当然スペクトルは一本です。スペクトルがずらし演算子であることがはっきりとわかります。また、周波数を上げるには局発に負の周波数、周波数を下げるには局発に正の周波数を選べばいいこともわかります。

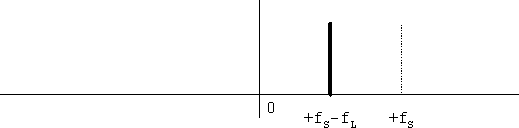
図6 出力信号のスペクトル

周波数変換を行う場合、図6を見てわかるように本来は解析信号同士で変換を行うことが合理的です。この場合、スペクトルが分裂しないことから送信機の不要輻射を心配しなくてもよいですし、受信機の場合はイメージ妨害の心配がなくなります。

実数と複素数による周波数変換

実際の回路では、局発を解析信号にすることはできても入力は普通の実信号であることがあります（ウェーバー方式がその例）。図7、8、9にその場合のスペクトルの変化を示します。

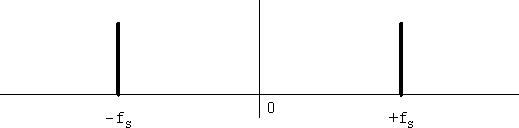
図7 入力信号のスペクトル

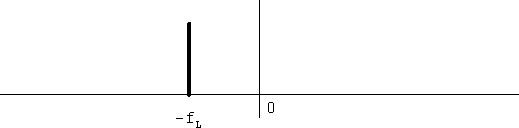
図8 局発信号のスペクトル

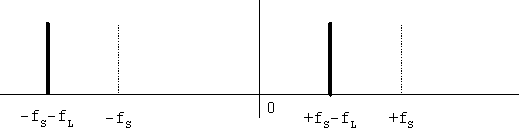
図9 周波数変換後のスペクトル

局発のスペクトルが一本しかないため片方向へのずらしになっていますが、元の信号にスペクトルが二本あるため、出力のスペクトルも二本あります。このため、複素数のまま出力を扱えばイメージ妨害などの問題はおきませんが、虚数部を捨てて実信号化を行うと、負の周波数成分と正の周波数成分が重畳されるため、実信号の周波数変換と同様の問題がおきます。そのため複素信号処理の利点を活用するには、最後に何らかの工夫をおこなって負の周波数からの妨害を避ける必要があります。

⇒次は複素プロダクト検波