同期検波

振幅変調の復調方式には包絡線検波のほかに同期検波と呼ばれるものがあります。以下ではこの方式について見てみましょう

包絡線を取り出す

まずはもう一度振幅変調のスペクトルを表す式を見てみましょう。

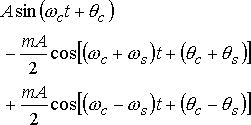
この式にsin(ω_ct+θ_d)をかけてみましょう。

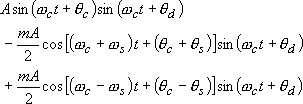
これを展開します。

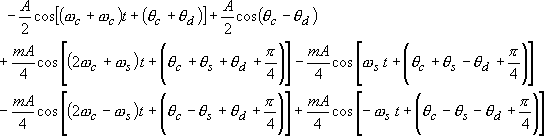
このスペクトルから角周波数が2ω_cの成分をLPFで取り除いて少し整理します。

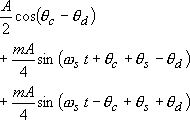
さて、得られた式でθ_d=θ_cとおくと打ち消しあって最終的に以下の式を得ます。

これはまさに変調信号そのものです。つまり、振幅変調波に対して、搬送波と同位相の無変調波を掛け合わせると信号を復調することができます。振幅が半分になっていますが、残りの半分は搬送波周波数2ω_cの振幅変調波となっています。

包絡線検波との関係

さて、同期検波は掛け算器で検波するわけですが、包絡線検波とまったく違う方式なのに同様に検波できることが不思議です。どうなっているのか調べてみましょう。

包絡線検波の要はダイオードによる負の電流の阻止です（整流）。このことからダイオード検波とも呼ばれます。ダイオードによる整流が同期検波と同じ結果を生む理由は図1を見ながら説明します。

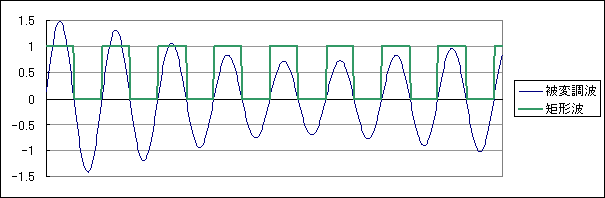
図1　ダイオード検波の別解釈

この図では被変調波に同期した矩形波が描かれています。矩形波は被変調波が正のとき1であり、負のときは0です。この両者を掛け合わせるとダイオード検波と同じく半波整流された波形が得られるのは容易に理解できます。一方、矩形波はその周波数の整数倍成分のスペクトルを含みます（0倍、1倍も含む）。このことから、矩形波を掛け合わせることによって基本波信号も掛け合わされていることが理解できます。矩形波の高調波の信号も同時にかけていますがそれは問題にはなりません。

この図から、ダイオード検波と同期検波がそれほどかけ離れたものではないことがわかります。では、同期検波とダイオード検波は同等かというとそうではありません。上のようにきれいに物事が運ぶのは雑音や妨害が一切ない場合です。実際には雑音や隣接チャンネルによって波形は乱れます。ダイオード検波の場合この乱れは受信信号のひずみになります。これは雑音や混信によって矩形波が被変調波と同期しないものになるためです。同期検波の場合このような問題はありません。

⇒次はフェージング式SSB変調