最適化

FIRフィルタのアセンブリ言語による実装は、それだけでC言語による実装より3倍も速いものになりました。これはひとえに循環バッファ・アクセスというC言語にない機能を活用したからです。しかしながら、絶対的なサイクル数を見るとまだ1タップあたり3サイクルかかっています。これはDSPプログラマとしては決して許容できる速度ではありません。そこで今回は前回作ったプログラムを改良してより高速のものに最適化していきます。

アクセス最適化

前回作ったプログラムのFIRフィルタ部を見ると、DOループの中に二つのロード命令が現れます（青い部分）。この二つは連続してあらわれていますのでうまくすればデュアル・ロード命令に変換できます。

        // input : ax0
        // output: mr1
fir:
    mr=0;                       // SUM=0
    dm(i0+=m0)=mx0;             // 最新のサンプルをストア
    cntr=TAPS;                  // TAPS回繰り返し
    do fir_loop until ce;
        mx0=dm(i0+=m0);         // ディレイラインのロード(古い物から新しい物へ)
        my0=dm(i6+=m5);         // 伝達関数のロード(後ろから前へ)
fir_loop:
        mr=mr+mx0*my0(ss);      // 積和
    mr=mr(rnd);
    rts;  

置き換えは。下のプログラムのように二つのロード命令をコンマで区切り、片方をPMロードに変更する(赤字の部分)のです。これで二つのロード命令をデュアル・ロードに変更できました。ただし、この変形をするために、もとのプログラムには次のような下ごしらえがしてあったことを見逃してはいけません。

• DMロードに使用するほうの命令は、もともとxopをデスティネーションにしていた
• PMロードに変更するほうの命令は、もともとyopをデスティネーションにしていた
• DMロードに使用するほうの命令は、もともとDAG1レジスタを使っていた
• PMロードに変更するほうの命令は、もともとDAG2レジスタを使っていた

このような準備をしていない場合、当然プログラムにはそれなりの変更を加えることになります。

        // input : ax0
        // output: mr1
fir:
    mr=0;                       // SUM=0
    dm(i0+=m0)=mx0;             // 最新のサンプルをストア
    cntr=TAPS;                  // TAPS回繰り返し
    do fir_loop until ce;
        mx0=dm(i0+=m0),my0=pm(i6+=m5); // ディレイラインと伝達関数のロード
fir_loop:
        mr=mr+mx0*my0(ss);      // 積和
    mr=mr(rnd);
    rts;  

さて、これだけで高速化することはできません。デュアル・ロード命令は確かに二つのオペランドに二つのバスを使って同時アクセスします。しかし、それはコアの話であって、実際に二つのオペランドが同時アクセス可能かどうかは別の話です。もし同時アクセス不能であればDSPはアクセスを直列化して解決を図ります。これでは速度は上がりません。

この問題を解決するため、オペランドを二つのメモリー・ブロックに分散配置します。ADSP-2191のメモリー・ブロックはアドレス空間で述べたように4つのバンクからなります。データ・ブロックは2バンクからなり、この二つのバンクに置いてあるオペランドは同時アクセスが可能です。この機能を活用するために、hを以下のようにdata2セクションに移します。標準のメモリー配置では、data1セクションとdata2セクションは別々のバンクに配置されるため、これによって同時アクセスが可能になります。

このプログラムはVisualDSP++3.0のものです。VisualDSP++2.0の場合もセクションdata2にhを移すことでデュアル・アクセスが可能になりますが、以下の.section/dm宣言を.section/pm宣言にしなければなりません(多分)。

            // フィルターのタップ数を宣言
#define TAPS 9
#define SAMPLE 20
            // データセクション
.section/dm data1;
.var delay[TAPS];  // ディレイライン
.var in[SMAPLE] = {0.5r, 0,0,0,0,0,0,0,0,0};   // 入力データ列
.var out[SAMPLE];                              // 出力データ列

.section/dm data2;
.var h[TAPS]={0.8r, -0.7r, 0.6r, -0.5r, 0.4r, -0.3r, 0.2r, -0.1r, 0.0r };  // 伝達関数

演算とロードの同時実行

いまやDOループの内部の命令は2つになっています。一つはデュアル・ロード命令であり、他方は積和命令です（下のプログラム）。このプログラムでは最初のデュアル・ロード命令でオペランドをロードし、次の積和命令でロードしたオペランドを使って演算しています。

    cntr=TAPS;                         // TAPS回繰り返し
    do fir_loop until ce;
        mx0=dm(i0+=m0),my0=pm(i6+=m5); // ディレイラインと伝達関数のロード
fir_loop:
        mr=mr+mx0*my0(ss);            // 積和

我々はデュアル・ロード命令と積和命令であれば演算とデュアル・ロード命令に置き換えることができることを知っています。しかしながら、上のプログラムを下のように変形することは適いません。

// 間違ったプログラム
    cntr=TAPS;                         // TAPS回繰り返し
    do fir_loop until ce;
fir_loop:
        mr=mr+mx0*my0(ss), mx0=dm(i0+=m0),my0=pm(i6+=m5);  // 積和とデュアルロード

このプログラムは間違っています。正常に動きません。命令後半のデュアル・ロード命令はmx0とmy0に値をロードし、積和演算は確かにmx0とmy0をオペランドとする演算を行います。しかし、このプログラムは今我々が思ったようには動きません。なぜなら、ロードの結果が有効になるのは次のサイクルだからです。もともとはロード結果をすぐ使いたくてこのように変形したのですから、命令の使い方が間違っていることになります。

このようにFIRフィルタ・プログラムの最後の詰めは容易な変形では克服できません。ここで必要とされるプログラミング技法はソフトウェア・パイプラインと呼ばれる方式であり、巧妙なデータのスケジューリングを必要とします。その結果プログラミングの敷居は高いものになっています。このような複雑な技法を使うには、正面から力技でせめても体力を浪費するだけで何らかの巧妙な方法を使わなければ大変な思いをします。

アナログ・デバイセズの日本語技術資料のページにアップロードされているEEJ-002「並行移動によるループ最適化」はこの問題向きの簡単な手法を紹介しています。ここで紹介されている方法は機械的な作業で最適化ができるのがメリットです。逆により高度な最適化手法の特殊な場合ですので複雑なアルゴリズムの最適化には向いていませんが、今回のプログラムには十分です。

下の図はその最適化手順を示したものです。この手法はロード⇒処理⇒ストア構成の手続きをループでまわすアルゴリズムの最適化に向いています。最適化手順は以下のとおりです。

• 最初に、オリジナルのプログラムはN回のループであると仮定します。下の図で鉤型の灰色の領域はそれが内包するコードを繰り返し実行するものと考えてください。このプログラムを用意するとき、LD（ロード）とST（ストア）の部分は同じレジスタを使わない構造にしておきます。
• まず最初の繰り返しと最後の繰り返しをループの外に出します。これによってループの繰り返しはN-2回になります。当然、プログラムの意味は変わりません。
• つぎに下の矢印にあるようにループ・ボディーの入出力と外に追い出したコードの入出力を交換します。この部分はこの手法の摩訶不思議な部分です。このようなことをすると動かなくなりそうですが、ロードとストアが異なるレジスタを使っているので実際には問題ありません。
• ステップ(c)で交換したコードを演算部と同時実行するように命令を変更する

単純な作業の積み重ねでちゃんと最適化できることが図示されています。

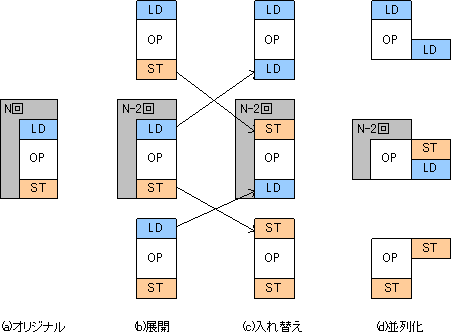
つぎにこの手法を使って我々のプログラムを最適化してみましょう。今回のFIRフィルタでは、デュアル・ロード命令が図のLD、積和命令が図のOPにあたります。STにあたる命令はありません。最後の再吸収のステップはもともとの説明にはありません。これはSTがないために、ループの前に追い出したコードがループボディーと同じ形になることから、再度ループボディーに吸収する変換です。この結果、ループ回数はTAPS-1回となります。

//
//  (a) オリジナル
//
    cntr=TAPS;
    do fir_loop until ce;
        mx0=dm(i0+=m0),my0=pm(i6+=m5); 

fir_loop:
        mr=mr+mx0*my0(ss);

//
//  (b) 展開
//
    mx0=dm(i0+=m0),my0=pm(i6+=m5); 
    mr=mr+mx0*my0(ss);

    cntr=TAPS-2;
    do fir_loop until ce;
        mx0=dm(i0+=m0),my0=pm(i6+=m5); 
fir_loop:
        mr=mr+mx0*my0(ss);

    mx0=dm(i0+=m0),my0=pm(i6+=m5); 
    mr=mr+mx0*my0(ss);

//
//  (c) 入れ替え
//
    mx0=dm(i0+=m0),my0=pm(i6+=m5); 
    mr=mr+mx0*my0(ss);
    mx0=dm(i0+=m0),my0=pm(i6+=m5); 

    cntr=TAPS-2;
    do fir_loop until ce;
        mr=mr+mx0*my0(ss);
fir_loop:
        mx0=dm(i0+=m0),my0=pm(i6+=m5); 

    mr=mr+mx0*my0(ss);

//
//  (d) 並列化
//
    mx0=dm(i0+=m0),my0=pm(i6+=m5); 
    mr=mr+mx0*my0(ss), mx0=dm(i0+=m0),my0=pm(i6+=m5); 

    cntr=TAPS-2;
    do fir_loop until ce;
fir_loop:
        mr=mr+mx0*my0(ss), mx0=dm(i0+=m0),my0=pm(i6+=m5); 

    mr=mr+mx0*my0(ss);

//
//  (e) 再吸収
//
    mx0=dm(i0+=m0),my0=pm(i6+=m5);                        // プリロード

    cntr=TAPS-1;
    do fir_loop until ce;
fir_loop:
        mr=mr+mx0*my0(ss), mx0=dm(i0+=m0),my0=pm(i6+=m5); // 積和

    mr=mr+mx0*my0(ss);                                    // 最後の積和

こうして最適化したコードをルーチンに組み込みます。ループの後ろに最後の積和が押し出されましたので、独立していた丸め命令を積和のオプションに押し込んで1サイクル削減します。最後にRTS命令を遅延分岐化して、積和命令をディレイ・スロットに配置します。足りない分はNOPで埋めます。NOPの分は余計なので、よく考えると丸め命令を削った意味はなくなっています。

        // input : ax0
        // output: mr1
fir:
    mr=0;                               // SUM=0
    dm(i0+=m0)=mx0;                     // 最新のサンプルをストア
    mx0=dm(i0+=m0),my0=pm(i6+=m5);      // プリロード

    cntr=TAPS-1;
    do fir_loop until ce;
fir_loop:
        mr=mr+mx0*my0(ss), mx0=dm(i0+=m0),my0=pm(i6+=m5); 

    rts(db);                            // 遅延分岐付の戻り命令


    mr=mr+mx0*my0(rnd);                 // 最後の積和。丸め命令を吸収している
    nop;

今回はアセンブリ言語で書いた命令を最適化してみました。今回説明したように最適化は方法によっては機械的な作業で済むこともあります。

次は⇒なぜ最適化できるか