なぜ最適化できるか

前回、ループの最適化の方法を説明しましたが、やや魔術的なその方法がなぜうまくいくかきちんと説明していませんでした。そこで、ちょっと予定を変えて背景となる原理を説明しておきます。

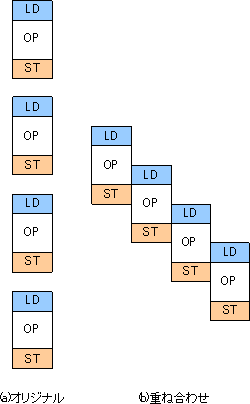
右の図の(a)はオリジナルのプログラムを展開したものです。この図は4回の繰り返しを展開したものですが、もともとのプログラムのロード⇒処理⇒ストアというながれを保ったまま素直に展開しています。繰り返しの数は4回ですが別に何回であっても展開の仕方は同じです。

(b)は同じプログラムに変形を加えたものです。繰り返しのそれぞれの処理は同じですが、一部重ね合わせています。例えば、1回目の繰り返しの処理の途中から、2回目の繰り返しのロードが始まっています。1回目の処理のストアが終わるのは2回目の処理の半ばです。そして、2回目の処理の半ばから3回目のロードが始まります。

DSPですから演算とロード/ストアを同時に行えるのはわかりますが、ロードとストアの順番がいれかわってもいいのでしょうか。その答えは、入れ替わってもいいようにプログラムしておくというものです。最適化の中で、「ロードとストアが同じレジスタを使わないようにしておく」という説明をしましたが、それがまさにこのための布石なのです。ロードとストアが異なるレジスタを使うのであれば、n回目の繰り返しのストアの前にn+1回目の繰り返しのロードを実行しても、n回目のストアが阻害されることはありません。これはすべての繰り返しに言えることですので、プログラムは問題なく動作します。

このような処理の結果、プログラムの実行速度は飛躍的に上がります。図の二つのプログラムはやや比較しにくいですが、一見しただけで重ねあわせを行った後のプログラムのほうが圧倒的に短いことがわかります。そして最近の汎用プロセッサとは異なり、DSPのプログラムは短いほど速いのです。これは強調してしすぎることはありません。x86などはプロセッサの世代ごとに同じアルゴリズムでも最適なコーディングは異なります。プログラマやコンパイラはプロセッサごとに最適の方法を見極めてコードを生成しなければなりません。しかし、DSPの場合世代が変わっても短いコードほど速いという直感的な判断が効くので、最適化の見通しはある程度楽だといえます。

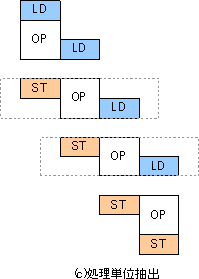
さて、重ね合わせの次に再びループに戻す作業が必要です。右の図の(c)はその様子を説明したものです。重ねあわせによってプログラムの構造はやや複雑になっていますが、上手に包丁を入れれば図のように処理の単位を綺麗に切り出すことができます。このように切り出せば、処理単位となっているコードが繰り返しであり、ループに変形できることは一目瞭然です。

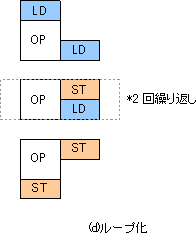
最後に取り出した処理単位を元にループを再構成しています。今回のループはもともと4回でしたが、図(c)から再構成の結果は2回のループになっていることがわかります。それにもとずいて描きなおしたのが図(d)です。この図には2回繰り返しと書いていますが、当然もともとN回の処理はN-2回となります。

最終的に得られた結果は最適化のページで説明した手続きが生成する結果とぴったりあっています。つまり、今回説明した方法を簡略化して機械的な手続きにしたのが前回の手法であるといえます。このように前回紹介した手法は機械的手続きで最適化が行えるにもかかわらず、背景にある考え方はしっかりしたものであり、安心して使えます。FFTのようなより複雑なアルゴリズムの場合、この方法を拡張した精密な手法が必要になりますが、基本的な発想は同じです。

次は⇒最適化の効果