FIRフィルタを式で表すと下のようになります。この式は信号処理にかかわる限りどこまでもついてくる式で、まず逃げて通ることはできません。実際のところ、この式はFIRフィルタというよりも「信号系の伝達関数のFIR表現」というべき広い意味を持った式です。それがこの式がいつも現れる理由です。
プログラマとしては式の意味など無視してとっとと実装してしまってもいいのですが、せっかくですのでこの式の物理的な意味を眺めて見ましょう。
この式の入力はx(n)です。入力は数列であり、nは時間に対応する添え字です。つまり時間が経つにつれ、nは0,1,2,3...と増えていきます。普通に目にする信号処理ではnに対応する時間は等間隔です。例えば、nが1増えるごとに時間が1μ秒増えるといった関係にあります。あたりまえのことだと思うのですが、どの教科書でも断ってあるあたりに不気味なものを感じないでもありません。
x(n)が入力ですので、中学校の数学から延々と叩き込まれた慣例通り出力は数列y(n)です。x(n)を図で表すと下の図のように離散的な時間に沿って変化する値を数列で表現したものだとわかります。
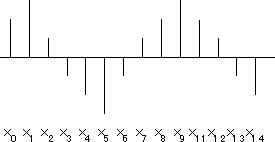
さて、この式の主役はh(k)で、これは系の伝達関数です。系にインパルスを入力すると伝達関数と同じ形の波形が出力されることから伝達関数はインパルス応答とも呼ばれます。インパルスも時系列ですので、下の図のように離散時間に沿って変化する値を数列で表現したものだとわかります。
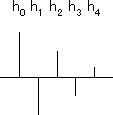
ここでインパルスδ(k)とは:
である関数です。つまりk=0のときは出力1で、それ以外の時には出力が0になりるような関数です。
数学に強い人ならば上の式は即座に理解できるのでしょうが、残念ながら筆者の場合初見から躓きました。ポイントはただ一点で「なんでxの式の媒介変数kは符号が負なんだ?」というのを理解するのに何年かかったかわかりません。要するに放っていただけですが、何事もイメージでなければ理解できない筆者には数式の意味を把握するにはどうしても式からイメージへの変換が必要でした。それにとまどったのです。
上の式を理解する鍵はまさに「kの符号が負」である意味を理解することにあります。それを理解するために少し回り道してh(k)がインパル応答であるという意味を考えてみましょう。h(k)がインパルス応答だというのは、何度も繰り返すようですが、系にインパルスを入力すると出力がh(k)になるということです。具体的な例を挙げましょう。
このように、非常に短い時間の入力(インパルス)に対する残響(応答)が、その系の伝達関数(インパルス応答)です。h(k)が残響ということは、例えばお寺の鐘の伝達関数をH1(k)で表すと、H1(k)はゴーンという音そのものであり、トライアングルの伝達関数をH2(k)で表すとH2(k)はちーんという音そのものです。
このことから、h(k)をもうすこし詳しく理解できるようになります。h(0)という値を考えてみましょう。これはインパルスが与えられたその瞬間の系の出力です。誤解を恐れずに言えば強さ1で鐘をついた瞬間の「ご」という音にあたります。次にh(1)はその次の瞬間(サンプル)の残響、h(2)はさらにその次の瞬間の残響…という具合に、h(k)は系にインパルスを与えてからの刻々の残響を記録したものといえます。
h(k)が残響そのものと理解できたことから、式の理解を一歩進めることができます。次はx(n-k)h(k)とはなにか考える番です。
まずx(n-k)について考えてみましょう。便宜的にnを「現在」と読み替えるとx(n-k)は「現在からkサンプル前の入力」と読むことができます。次にh(k)ですがこれはすでにインパルス入力に対するkサンプル後の残響であることがわかっています。ここからx(n-k)h(k)とはkサンプル前に発生した入力のkサンプル後の残響ということがわかります。言葉を変えると「kサンプル前の入力の現在における残響」ということになります。
これを図示したのが下の図です。h(0)がx(6)と対応していることから、この図はx(6)が入力されたときの系の内部状態を表しています。1サンプル前の入力値x(5)と対応するのが1サンプル過去のインパルスに対する係数h(1)、2サンプル前の入力値x(4)と対応するのが2サンプル過去のインパルスに対する係数h(2)…となっているのが見て取れます。
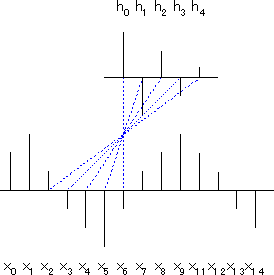
そしてこの対応を保ったまま見やすくなるように変形したのが下の図です。この図は入力信号の時間軸をx(6)を中心に反転させています。このように、過去に発生したインパルをある時点で整理すると、xの時間軸を逆転させたものをhが綺麗に対応しています。これが最初の式でkの符号が負であることの図形による説明です。
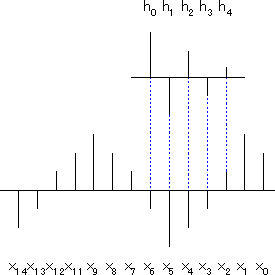
もう一度全体を眺めてみましょう。すでに式の後半は「kサンプル前の入力の現在における残響」ということが理解できています。
その総和とは、「現在からN-1サンプル前の入力が現在に残している残響の総和」です。平たく言えば過去の入力の残響の重ね合わせです。なんのことはありません。すごくあたりまえのことを言っているだけです。最後に式全体を言葉で言い表すと、「nサンプル目の出力は、そこからさかのぼることN-1サンプル前までの入力が残している残響を重ね合わせたもの」です。
除夜の鐘は108回つきます。十分に特性のいい鐘の場合、最後の鐘を打ち終わったときの音色は108回の打うちならしが起こした残響の総和を聞いていることになります。これが上にあげた式の意味であり、畳込みとは残響の重ねあわせであることがわかります。
フィルターとは特定の周波数だけを通す、あるいは遮断する回路です。それらの回路は残響特性をもっています。DSPでフィルターを実装する場合、この残響特性をシミュレートすることで任意の伝達関数をもったフィルターを実現します。そして、シミュレートに使うアルゴリズムが畳み込みであり、上の式です。これがFIRフィルターの物理的な意味です。
次は⇒C言語による実装