ポリフェーズ分解

今回は少し趣向を変えて数学的な話になります。「もともとプログラムのコーナーのくせに数学が多すぎるぞ」という非難が聞こえてきそうですが、まぁ信号処理はそのあたりも楽しみのひとつとあきらめてください。少しばかりの数学なら知的な遊びのうちです。

図1はインパルス応答h[k]です。プログラマがこのような列を見ると、即座に数列として捕らえます。実際、プログラムに書くときにはこのようなデータ列は配列として表現します。

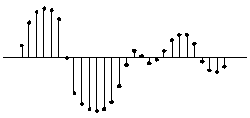
図1 インパルス応答

そこで、このインパルス応答をそのまま数列であらわすと、

h[k] = h0, h1, h2, h3 ... 

と、なります。このように数列としてインパルス応答を表現するのは直感的にわかりやすいのですが、数学的な操作という点から考えると少し扱いづらいところがあります。そこで、これをz変換を使って扱いやすい形式に変更します。z変換が何かについては教科書を読んでもらうとして、ここでは次のようなものとして考えてください。

• 数列を変数zの多項式にする
• k番目の項の変数はz^-k

このような変形を施すと、上のh[k]は次のようになります（"^"はべき乗演算子）。

H[z]=Z{h(k)}= h0 + h1*z^-1 + h2*z^-2 + h3*z^-3 +...

z変換を施すことにより、インパルス応答を表す数列は単一の多項式になります。多項式に変形したことによりインパルス応答に対していろいろな演算を行えるようになります。個人的に面白いなと思うのは

• z変換した信号列（あるいはインパルス応答）にz^-1を乗ずると、全体が1サンプル後ろにずれる
• z変換した信号列にz変換したインパルス応答を乗ずると、フィルターを通したのと同じ演算をおこなえる

といった点です。z変換の話はともかく上の式を変形してみましょう。

H[z]= h0 + h1*z^-1 + h2*z^-2 + h3*z^-3 + h4*z^-4 +...
    = h0 + h2*z^-2 + h4*z^-4 + h6*z^-6... + h1*z^-1 + h3*z^-3 + h5*z^-5 + ...
    = E0[z] + z^-1*E1[z^2]
ここで
   E0[z]=h0 + h2*z^-1 + h4*z^-2 + h6*z^-3 + ....
   E1[z]=h1 + h3*z^-1 + h5*z^-2 + h7*z^-3 + ....

と、このようにH[z]を偶数番目の係数からなるフィルターと奇数番目の係数からなるフィルターの和としてあらわすことができるとわかります。この場合、和は回路上では並列に配置されたフィルターの出力の和として実現されます。

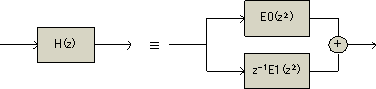
図2 分解したフィルターの接続

このように分解したフィルタは、元のフィルターの偶数番目の係数しか持っておらず、かつ次数がもとのフィルターの半分に減っています。これはもとのフィルターを位相に基づいて分解したものと考えられ、ポリフェーズ分解と呼びます。上の例は元のフィルターを二つに分解しましたが、もちろん任意のN個に分解することもできます。

次は⇒ポリフェーズ フィルタ