ノーブル恒等変換

前回と前前回では説明を飛ばしてしまいましたが、アップサンプリングとダウンサンプリングの記号があります。

ブロック記号

ダウンサンプリングは下の図のような記号です。下向き矢印はこれがダウンサンプリングであることを表し、記号Mは1/Mのダウンサンプラであることを示します。

また、アップサンプリングは下の図のような記号です。上向き矢印はこれがアップサンプリングであることを表し、記号LはL倍のアップサンプラであることを示します。

ノーブル恒等変換

ノーブル恒等変換( Noble Identity )はこの項のネタ本である「シミュレーションで学ぶディジタル信号処理」（尾知博、CQ出版社）で紹介されている関係です。ネット上で検索してみると米国のサイトでは比較的ヒットしますが日本ではあまりヒットしません。

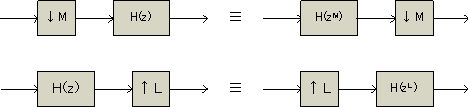
本では「このような関係がある」としか書いてありませんでしたが、最初は頭を抱えてしまいました。アップサンプリング・ダウンサンプリングの前後でシステムを動かすと、エイリアス・スペクトルはどうなるのか心配だったからです。しかし、そういう心配をしたのはZ変換に対する理解が甘かったためで、実際にはこの場合心配はありません。

アップサンプリングの場合を例にとって考えてみましょう。アップサンプラの前にある信号処理段H(z)が、アップサンプラの後ろに移されると、その処理がH(z^L)になります。ここでz変換の基礎から説明することはできませんが、H(z)が1サンプル毎の処理ならばH(z^L)はLサンプル毎の処理ということです。

前前回のアップ･サンプリングで、アップサンプリング後は必ずLPFをかけなければ高調波に悩まされると説明しましたが、今回のノーブル恒等変換にはその手のフィルタがありません。いいのでしょうか？　

いいのです。

アップ･サンプリングでLPFが必要なのは、後段でサンプルごとの処理を行うという仮定があるからです。対して今回後段に回されたH(z^L)はLサンプル毎の処理しかしません。そこでH(z^L)とその入力の関係をまとめてみると。

アップサンプラは1個のデータを出力し、次にL-1個の0を出力する。
H(z^L)は1個の入力を処理し、続くL-1個の入力を無視する。

直感的に両者の入出力がかみ合っていることがわかります。実際には位相がきちんと合っていないと出力が0になりますが、それさえ注意すればノーブル恒等変換が主張していることが奇抜でもなんでもないことは理解できます。同様の論議はダウンサンプリングの場合にも成り立ちます。

以上の話はポリフェーズ・フィルタへとつながっていきます。

次は⇒ポリフェーズ分解