関数表を工夫する

DDSの誤差を小さくするには位相精度を高めなければなりません。ところが、それには大きな正弦関数の表が必要になります。ざっくり言って16ビットDSP用の表なら65536点の要素をもちたいところです。このような表は現実的ではありませんので、より小さい表を使うことを考えます。

三角関数の公式

表を小さくする一番合理的な方法は、単一の表を二つに分解することです。高校で習った三角関数の公式が役に立ちます。

SIN(A+B) = SIN(A) COS(B) + COS(A) SIN(B)

この公式を使うと、円周を256分割する位相量Aとそれをさらに256分割する位相量Bから正弦と余弦を求め、それらから円周を65536分割する正弦関数を合成できます。このあたりの操作を模式化して図1に示します。

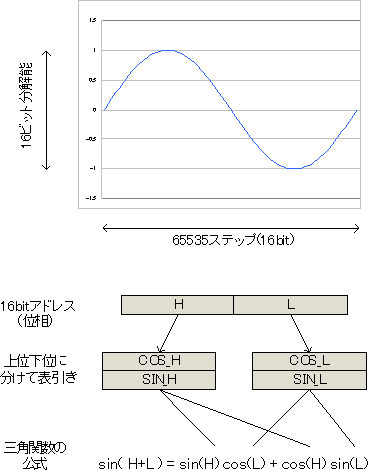
図1 位相を分割して関数を再合成する

この方法は正弦関数表のほかに余弦関数表が必要になります。しかし素直に実装しても65536エントリーの表が256エントリーの表×4で済むため、1024エントリーで実装することができます。

実装

アセンブリ言語による実装を以下に示します。

このプログラムはC言語から呼ぶサブルーチンです。16ビットの符号なし整数を位相として受け取り、16ビットの符号付整数を返します。4つの256エントリーの表は外部のデータをアセンブル時にテキストとして読み込んで初期化します。データは表計算ソフトで作りました。

アルゴリズムは直線的でこれといったひねりはありません。16ビットの位相を上下8ビットに分割して表引きのインデックスとします。

// 符号なし整数を位相として受け取り、振幅を整数で返す
// int sin_int( unsigned int );
#include <asm_sprt.h>
.section/dm data1;
.var sina[256]="sinh.txt";
.var cosa[256]="cosh.txt";
.var sinb[256]="sinl.txt";
.var cosb[256]="cosl.txt";

.section/pm program;
.global _sin_int;
_sin_int:
        entry;                          // スタックフレーム確立
                        // 16bit位相量を8bitのインデックスに分解
        get_arg_dreg(ax0, 1);           // 引数を取得
        ay0=0x00ff;
        ar=ax0 and ay0;
        m1=ar;                          // 下位8bit;
        sr = lshift ax0 by -8(lo);
        m3=sr0;                         // 上位8bit;
        
                        // 正弦、余弦表をアクセス
        i1=sina;
        mx0=dm(i1+m3);                  // sin(h)
        i1=cosa;
        my0=dm(i1+m3);                  // cos(h)
        i1=sinb;
        mx1=dm(i1+m1);                  // sin(l)
        i1=cosb;
        my1=dm(i1+m1);                  // cos(l)
        
                        // sin(a+b)=sin(a)cos(b)+cos(a)sin(b)
        dis m_mode;                     // 固定小数点モード
        mr=mx0*my1(ss);
        mr=mr+mx1*my0(rnd);
        sat mr;
        ax1 = mr1;
        ena m_mode;                     // 整数モードに戻す

        exit;                           // スタックフレームを廃棄

誤差の評価

ここでいう誤差とは位相誤差を含まない純粋な振幅誤差です。つまり合成される表が提供する位相と同じ点で正弦関数の値を計算し、それを表中の値と比較します。誤差の評価は次のように行いました。

C言語でプログラムを書き、65536点全部のデータを計算する
計算したデータをテキスト形式でファイルに出力する
表計算ソフトで正弦関数を計算し、読み込んだテキストファイルと比較する。

こうして計算した誤差を以下に示します。表中の単一のデータは±0.5LSBの誤差を持ちます。図2に表れている定常的な短周期の誤差がこれです。

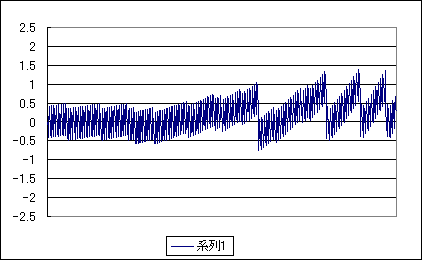
図2 最初の1024点の誤差

図3は第一象現の誤差です。上の三角関数の公式を実装すると、次のような誤差が入ってきます。

分割したそれぞれの表のデータは±0.5LSBの誤差を持つ。
各項を計算する乗算では誤差は混入しない。項自身の誤差は乗算により±0.5LSBよりわずかに増える。
加算によって互いの誤差が足しあわされる。誤差は±1LSBを少し超える。
最後に丸めによって±0.5LSBの誤差が足される。

図3のグラフによると誤差の最悪値は±1.5LSBを少し超える程度であり、これは上の考察によく一致しています。

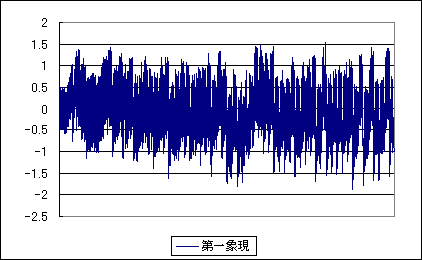
図3 最初の16384点の誤差

次は⇒ラッパークラス