DDSの位相誤差

前のページでは1KHz用に作った正弦波テーブルから900Hzを生成したところ予想以上に音の濁りが大きいという結果になりました。この理由を考えてみましょう。

位相誤差と振幅誤差

前回はもともと1KHz用に作ったテーブルを利用するため、DDSアルゴリズムを使って900Hzの正弦波に変換しました。この変換は波形の補間などはせず、純粋に位相だけを積み上げていって表引き用の添え字を整数化することによる変換でした。

ここで整数化は単なる切捨てであり、位相の切捨ての分は瞬時の位相誤差です。切捨てによる位相誤差は累積こそしませんが、瞬間的にはそれなりの大きさになります。そして、理想波形と比較すると位相誤差は振幅誤差として現れます（図1）

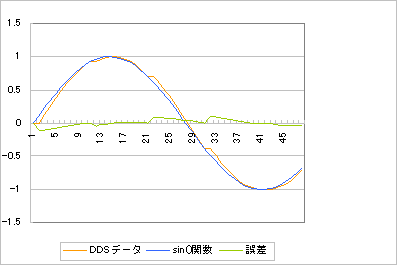
図1 生成したデータと誤差

このデータ比較は位相の切り捨てで作ったデータを使っています。切捨ては実際には位相が少しだけ遅れますので上の波形の重ね方を変えてみると次のようになります。

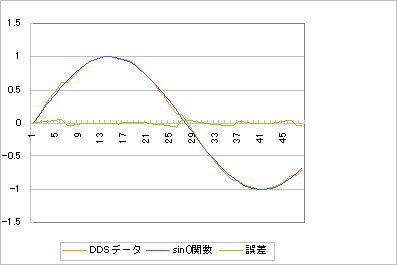
図2 位相遅れを修正したデータでの比較

この状況での振幅の誤差は±5%ほどあります。これが音のにごりの正体です。誤差=雑音ですが、この場合は周期性があるためにごって聞こえるのです。元の信号に比べて雑音の大きさが-26dBもあるわけで、聞こえないはずがありません。

濁りを消すには？

位相誤差が振幅誤差となり、それが濁りとなって聞こえることがわかりました。そこで濁りを消すには位相誤差を無くせばいいということになります。ではどれくらい位相誤差が小さければよいのでしょうか。それを調べるにはsin関数の傾きを調べなければなりません。

xをパラメーターに正弦関数sin(x)の表を作るとしましょう。xを等間隔にとるとしてxの誤差(位相誤差)εによって得られる値はsin( x+ε )となります。これによって振幅誤差が生じます。単位位相誤差あたりの振幅誤差を得るには、sin(x)を微分すればいいことはすぐわかります。sin(x)の導関数の絶対値が大きいところでは位相誤差が大きな振幅誤差になるわけです。

正弦関数の導関数の絶対値は関数値が0と交わる点で最大になります。代表的な点としてx=0を考えましょう。このとき、微分値は以下になることが有名です。

( at x=0 )

ここでxの単位はラジアンです。正弦関数の1周期は2πラジアン、正弦関数の値の範囲は±1です。位相誤差と量子化誤差を最小にするために両者を16ビットであらわすことにし、xの1 LSBに相当するsin(x)の変化量を計算するとπ LSBとなります。

図3で考えてみてください。これは辺の大きさが±1の正方形に正弦波を押し込めたときの図です。中央を斜めに走っているのは傾きがπの直線で、これが正弦波に接していることがわかります。この正方形の辺の大きさが±32768であっても図形は相似のままで、やはり接線の傾きはπです。つまり横軸1 LSBに対して原点付近では縦軸もπ LSBだけ変化するということです。

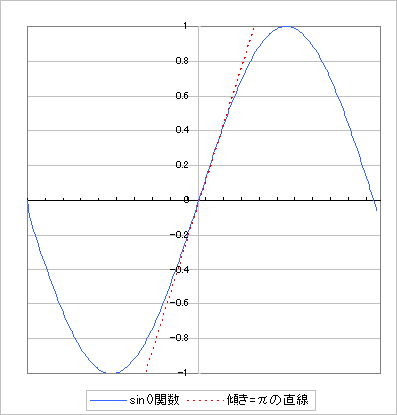
図3 正弦波とその接線

この結論から、位相誤差が0.5 LSBならば振幅誤差の最大値はおよそ1.57 LSBとなります。これは1ワードが持つ雑音のフロアレベルよりも6db (1 LSB)ほど大きな値になります。xを16ビットで打ち切ったことによる誤差は、sin関数の出力の1.5 LSB分としてあらわれ、このことは出力の有効ビット数が15ビット（符号1+有効数字14）に落ちていることを意味します。

正弦関数表

15ビット精度で十分かどうかは別としてこの表を作ってみましょう。しかしそれはADSP-2191では無理な相談です。引数の範囲が16ビットであるような表は大きさが64KWになってしまい、これは内蔵メモリーを食い尽くしてしまいます。できません。仮に外部メモリーとして実現するとしても、合理的でも美しくもありません。

そこで代案を考えてみることにします。

次は⇒関数表を工夫する