デシメーター
VisualDSP++4.0のfir_decima_fr16()は、デュアル演算を使用していません。そのため、周波数分の性能しかでません。そこで、デュアル演算を使用して倍速で動作するデシメーターを組みました。
デュアル演算化
デシメーターは、FIRフィルタをRサンプルおきに動作させるものと考えることが出来ます。ここでRはダウンサンプル比で、動作させないR-1サンプルに関しては、単に遅延線変数(状態変数)にサンプルを格納します。
結論から言うと、いろいろな事情があって内部のFIRフィルタをそのままデュアル演算化することは出来ません。そこで参考文献1(*)で紹介されているマルチチャンネル化を行います。マルチチャンネル化とは、簡単に言うとそのままでは並列演算を適用できないデータストリームを変形して、擬似的に複数のストリームとしてしまうことです。これによって並列演算、デュアル演算を適用できるようになります。
マルチチャンネル化するには、データのどの部分を並列化するか見極めなければなりません。ここはあれこれデータの形をいじくって試行錯誤しながら考えることになります。今回は連続する二つの出力データを同時に計算することにしました。
ダウンサンプル比Rのデシメーターで、連続する二つの出力データを同時に計算するということは、現在の入力に対するインパルス応答と、Rサンプル過去の入力に対するインパルス応答を同時に計算するということです。つまりΣx(t-n)h(n)と、Σx(t-n+R)h(n)を同時に計算することになります。しかしこのままではx(t-n)とx(t-n+R)がばらばらの位置にあるため一括ロードができず、どう頭をひねっても高速化はできません。力技で状態変数を二つ持つ方法もありますが、少しオーバーヘッドが大きくなります。そこで違う場所をひねって逃げます。元の式を変形してΣx(t-n)h(n)と、Σx(t-n)h(n-R)にします。こうすると、同じデータに対して二つの異なるFIRを適用する形になります。これなら簡単にマルチチャンネル並列化が可能です。
h(n)と、h(n-R)は、単純に波形を横にずらしただけですから、図1のように簡単に並列化できます。
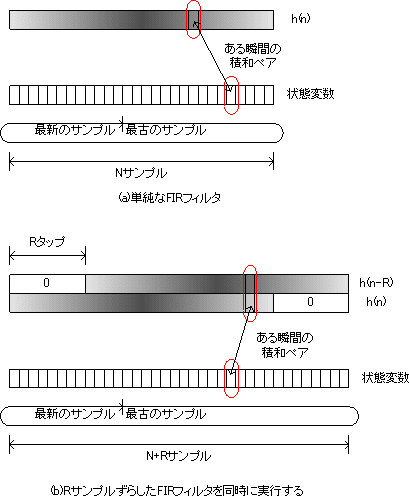
図1 Rサンプル離れた二つのサンプルを同時処理する
この方法は比較的わかり易いですが、残念なことにインパルス応答用のメモリがSIMD実装の場合の倍以上必要になります。また、状態変数もRサンプル分余計に必要になります。
実装
いったんデータ構造が決まれば実装は簡単です。インパルス応答の係数配列(coeff)からは16ビットデータを2ずつロードし、状態変数からは1サンプルずつロードします。coeffに格納するh(n)とh(n-R)は1サンプルごとにインターリーブして配置しておきます。そうしないと一回のロードで両方を取り出すことが出来ません。以下に最適化前のプログラムを示します。outerLoopの前半は入力配列から2Rサンプルのデータを状態変数に書き込みます。後半はFIRフィルタの実行です。実装上の理由で、一度に処理する入力サンプルの量はRの偶数倍でなければなりません。また、フィルタのタップ数は2Rより大きくなければなりません。
// Here, all variable is ready
// P0 : TAPS+R
// P2 : R
// P3 : out
// P4 : in
// P5 : countBy2R
// i0, b0, l0 : coeff
// i1, b1, l1 : delay line
i0 -= 4; // coeff points oldest one
loop outerLoop lc0 = p5; // loop countBy2R times
loop_begin outerLoop;
// copy 2R samples iinto delay line
loop copy2RSamples lc1 = p2; // loop R times;
loop_begin copy2RSamples;
r0 = [p4++]; // get 2 samples from in buffer
[i1++] = r0; // store 2 samples to delay line
loop_end copy2RSamples;
// now delay line pointer is set to oldest one
// core FIR filter
a1 = a0 = 0; // clear accmulator
loop doFIR lc1 = p0; // loop TAPS +R times
loop_begin doFIR;
r0 = [i0--] || r1.L = w[i1++];
a1 += r0.H * r1.L, a0 += r0.L * r1.L;
loop_end doFIR;
r2.H = a1, r2.L = a0;
[p3++] = r2; // store output
loop_end outerLoop;
上のプログラムの内側の二つのループにソフトウェア・パイプライン化を施したのが下のプログラムです。いずれのループもボディサイズが1サイクルになっています。
p0 += -1;
p2 += -1;
// Here, all variable is ready
// P0 : TAPS+R-1
// P2 : R-1
// P3 : out
// P4 : in
// P5 : countBy2R
// i0, b0, l0 : coeff
// i1, b1, l1 : delay line
i0 -= 4; // coeff points oldest one
loop outerLoop lc0 = p5; // loop countBy2R times
loop_begin outerLoop;
// copy 2R samples iinto delay line
r0 = [p4++]; // get 2 samples from in buffer
loop copy2RSamples lc1 = p2; // loop R-1 times;
loop_begin copy2RSamples;
r0 = [p4++]|| [i1++] = r0;
loop_end copy2RSamples;
[i1++] = r0; // store 2 samples to delay line
// now delay line pointer is set to oldest one
// core FIR filter
a1 = a0 = 0; // clear accmulator
r0 = [i0--] || r1.L = w[i1++];
loop doFIR lc1 = p0; // loop TAPS+R-1 times
loop_begin doFIR;
a1 += r0.H * r1.L, a0 += r0.L * r1.L || r0 = [i0--] || r1.L = w[i1++];
loop_end doFIR;
r2.H = (a1 += r0.H * r1.L), r2.L = (a0 += r0.L * r1.L);
[p3++] = r2; // store output
loop_end outerLoop;
ループ中ほどのアキュームレータのゼロクリア命令は、0を格納しているレジスタの掛け算命令に置き換えることで直前のロード命令と並列実行できるようになります。また、外側のループにソフトウェア・パイプライン化を施すと、ループボディ先頭と末尾の命令を同時実行できるようになります。しかし、可読性の低下に見合う性能向上をもたらさないのでそのままにしています。
参考
- 「Blackfin(ADSP-BF533)活用ハンドブック」CQ出版社。14章。